ГлавнаяО компанииСтатьи и публикации

1. Введение

На попытку применения знаний по вибродиагностике в анализе переходных процессов в электродвигателях переменного тока меня подвинула статья «Оценка степени деградации ротора серводвигателя с помощью Фурье анализа сигнала тока».

Для определения технического состояния трехфазных электродвигателей по токовым параметрам пусковых переходных процессов был использован переносной компьютер с платой ввода данных E440 фирмы LCard. Запись сигналов тока и напряжения во всех трех фазах проводились синхронно с частотой дискретизации 10 000 Гц, для ускорения процесса подключения к двигателю применялись токовые клещи, что позволило не разрывать цепи питания.

Для обработки сигналов был выбран пакет MathCad, который обеспечивал большую мощность, гибкость, компактность и наглядность процессов обработки. В пакете MathCad привлекало наличие большого количества встроенных функций обработки и визуализации расчетов, возможность принимать файлы распространенных форматов: text, Microsoft Excel, Lotus 1-2-3, MATLAB, dBaseIII.

Записанные компьютером сбора данные экспортировались в текстовые файлы, которые затем переносились на лабораторный компьютер обработки.

При среднем времени испытания порядка 1-3 минут, в одном канале записывается около 0,6-1,8x10⁶ точек, что обусловило достаточно большие (до 40 Мб на канал) размеры выходных текстовых файлов.

Меньшие размеры файлов были получены применением стандартного звукового формата WAV, который, кстати, «понимает» MathCad; еще большего сжатия данных удалось получить с использованием широко распространенного музыкального формата MP3. Такой формат был бы актуален для передачи данных по линиям связи, но процесс преобразования получился слишком громоздким в конкретных условиях. Максимальная ошибка восстановления из mp3 составляла не более 0,5 %, что вполне достаточно для решения поставленной задачи.

Для самой длительной реализации шесть исходных текстовых файлов «весили» 190 Мб, шестиканальный WAV имел размер 38,7 Мб, итоговый MP4 «тянул» всего 5,1 Мб.

2. Ввод и предварительный просмотр данных

В начале попробуем прослушать записанные сигналы, для чего переведем Ua и Ia в звуковой формат.

Определим число уровней квантования, которое, в свою очередь, и определяет максимальное выходное напряжение цифроаналогового преобразователя звуковой карты.

Resolution:=16

Сформируем первый канал из напряжения Ua. Для исключения потери динамического диапазона разделим каждую точку сигнала на размах варьирования выборки, который определяется как разность максимального и минимального значений. Затем отнормированный таким образом сигнал умножаем на число уровней квантования.

Добавим второй канал Ia, также выполнив нормировку на размах варьирования.

Запишем полученный «стерео» сигнал. Для функции записи частота дискретизации должна быть безразмерной величиной, поэтому SampleRate делим на Hz.

Полученный звуковой файл можно прослушать непосредственно из MathCad, вставив командами Insert/Object/«Звуковой файл». Появится иконка выбранной программы воспроизведения звука, нажав на который услышим звук включаемого вентилятора: в левом канале напряжение, в правом канале - ток.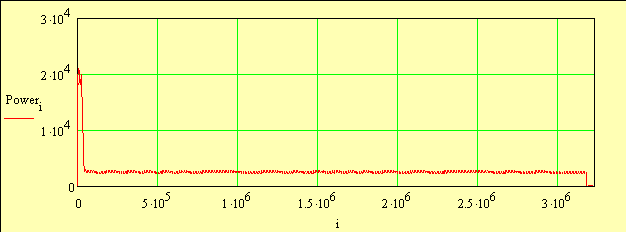

Рисунок 1. График мощности двигателя

Вообще-то ничего интересного, на первый взгляд, мы не услышим: обычный фон переменного тока 50 Гц, который через пять секунд становится едва слышимым в канале тока. Если внимательно вслушаться в первые пять секунд - можно заметить слабый, растущий вверх по частоте свист. Потом слышен обычный фон переменного тока 50 Гц, похожий на звук работающего вблизи мощного электродвигателя с какими-то мелкими призвуками и незначительными регулярными колебаниями уровня с периодом порядка 1 с. Если поднять уровень звука до возникновения легкого перегруза усилителя-колебания уровня становятся очень заметными. Это, вообще говоря, должно свидетельствовать о наличии биений между частотой 50 Гц и частотой вращения, и/или модуляции (скорее всего, амплитудной) тока 50 Гц. На спектрограмме с прямоугольным взвешивающим окном ничего этого не видно. С другими взвешивающими окнами (Hamming, Hanning, Blackman) хорошо видны две линии ниже сетевой частоты 50.049 Гц на 1.469 и 2.918 Гц, что позволяет использовать их в качестве диагностических параметров. Впрочем, это тема другого разговора.

Теперь перейдем к численному анализу. Определим мгновенную мощность двигателя как сумму мощностей в каждой фазе

и построим график мощности двигателя (рис. 1).

Здесь по оси X указаны номера точек, что не очень удобно для оценки характерных интервалов времени процесса. Поэтому введем вспомогательную переменную T и перейдем к представлению графиков в реальном времени.

Примечание: опытным путем было установлено, что максимальное число точек графика параметрически задаваемых функций вида x=X(t), y=Y(t), должно быть меньше 500 000.

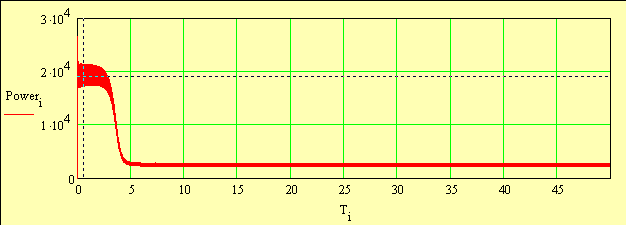Рисунок 2. График мощности двигателя

График мощности двигателя представлен на рис. 2.

С помощью встроенной фукции «X-Y TRACE» и «мышки» определим по графику время выхода двигателя на рабочую мощность и величину пусковой мощности.

Примечание: черными пунктирными линиями выводятся маркеры «X-Y Trace», координаты которых командами Copy/Paste передаются переменным.

3. Расчет пусковых параметров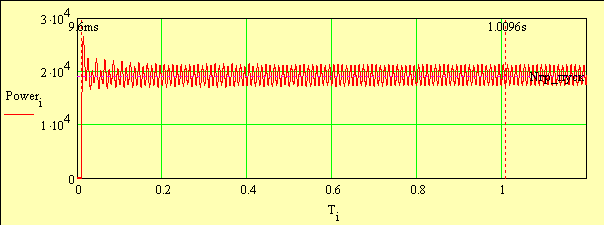

Рисунок 3
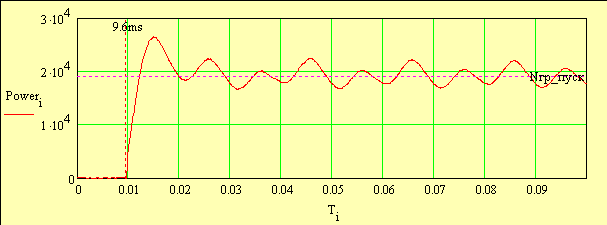Рисунок 4

Для более точного определения пусковых параметров построим график первой секунды пуска, выведем маркер средней пусковой мощности (рис. 3). На этом графике видно, что кривая мощности начинается на 9.6 mc от начала регистрации процесса. Для наглядности еще больше «растянем» график (рис. 4).

Введем обозначения и значения, полученные с помощью функции «X-Y TRACE»:

Пусковая мощность определяется как среднее значение на заданном интервале пуска, а действующее значение тока и напряжения определяются как средние по фазам среднеквадратичные значения по следующим формулам:

j0 := t_нач_пуск SampleRate	начальная точка расчета пусковых параметров
J :=( t_нач_пуск + Δt_пуск) SampleRate	конечная точка расчета пусковых параметров
	пусковая мощность
	среднее действующее значение пускового напряжения
	среднее действующее значение пускового тока

Получаем следующие значения пусковых параметров:
Nпуск = 19.2 kW
Uпуск = 189.2 V
Iпуск = 52.4 A
t_пуск = 5.2 s

Погрешность графического определения пусковой мощности относительно расчетной составила

(Nпуск - Nгр_пуск)/ Nпуск = -0.38%

4. Расчет рабочих параметров

Проделаем аналогичные вычисления для рабочих параметров. Построим график мощности на интервале Tраб, Траб+Δt_раб (рис. 5).

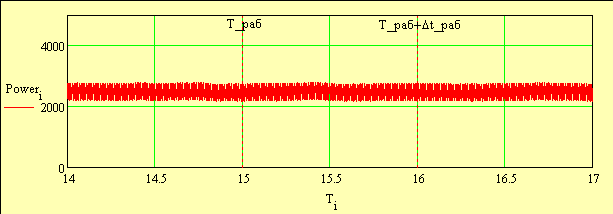Рисунок 5

Определим по графику «мышкой» с помощью функций «X-Y TRACE» и «Zoom» рабочую мощность

Nгр_раб := 2.433 x 103W Nгр_раб = 2.4 kW	рабочая мощность по графику
j0 := Т_раб·SampleRate	начальная точка расчета рабочих параметров
J := (Т_раб + Δt_раб) ·SampleRate	конечная точка расчета рабочих параметров
	рабочая мощность (средняя)
	среднее действующее значение рабочего напряжения
	среднее действующее значение рабочего тока
Nраб = 2.46 kW Iраб = 4.8 А Uраб = 212.5 V
Nполн := 3Uраб ·Iраб Nполн = 3.0 kW	полная мощность двигателя
cos φ := Nраб / Nполн cos φ = 0.81	коэффициент мощности

Погрешность графического определения рабочей мощности относительно расчетной составила

(Nраб - Nгр_раб) / Nраб = 1.23%

5. Расчет частоты напряжения питания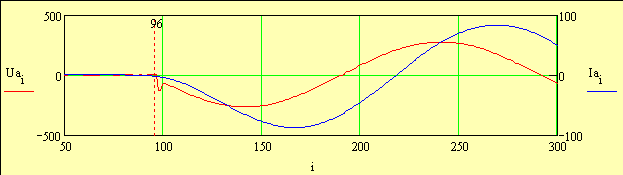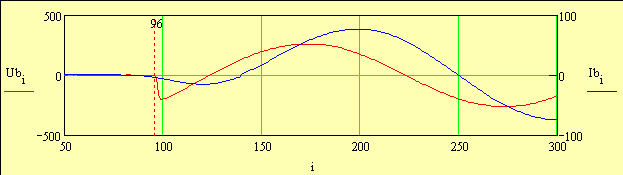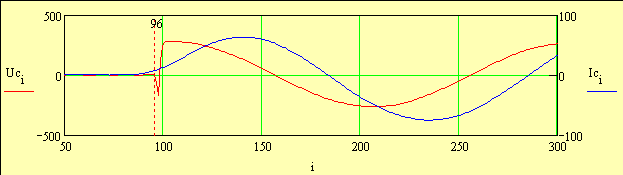

Рисунок 6

Для корректного проведения частотного анализа напряжения, тока и мощности необходимо получить передаточную амплитудно-частотную характеристику соответствующих датчиков, однако на момент проведения работ этого выполнено не было. Эту проблему еще предстоит решить, но просто беглое сравнение момента включения двигателя показывает, что сигнал тока практически не реагирует на скачок пускового напряжения, что и показано на следующих графиках (рис. 6).

Теперь рассчитаем спектр сигнала напряжения Ua с использованием встроенной фукции быстрого преобразования Фурье.

fсети := 50.049 Hz с помощью функции X-Y TRACE определяем частоту сети (рис. 7).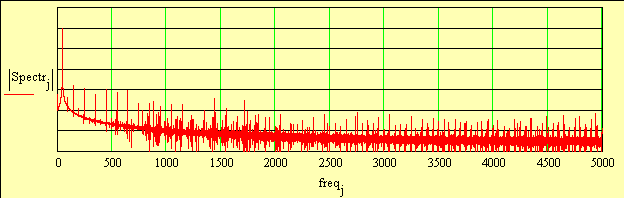

Полный спектр напряжения фазы «А»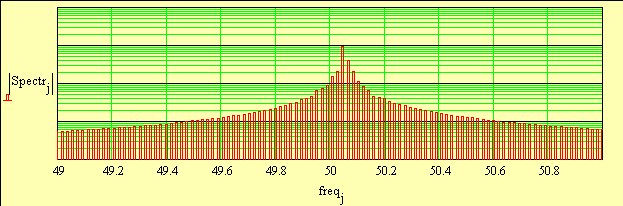

Спектр напряжения фазы «А» в окрестности 50 Гц

Рисунок 7

Осталось оформить итоговый протокол испытаний, отпечатать и передать Заказчику.

6. Выводы

1. Пакет MathCad предоставляет большие возможности параллельной обработки больших массивов информации, легко «переваривая» 6*3000000=18 000 000 и выводя на график 3 000 000 точек. Максимальное число линий спектрального анализа 2¹⁸=262144.

2. Спектральный анализ быстро и наглядно выполняется встроенными функциями быстрого преобразования Фурье. В пакете «SIGNAL PROCESSING EXTENSION PACK» представлено десять взвешивающих окон («Signal Windowing»), которые в данном примере не применялись, есть функции рассчета спектра мощности, кросс-спектров, кепстров, вейлвет-анализа, имеется возможность сглаживания и цифровой фильтрации различными типами фильтров. Всего этом приложении около 80 функций.

3. Пакет предоставляет очень разнообразные, гибкие, компактные и, вместе с тем, весьма наглядные средства построения алгоритмов обработки данных. Он очень удобен для предварительной отработки алгоритмов с тем, чтобы потом делать узкоспециализированное жестко ограниченное программное обеспечение под какую-то конкретную задачу.

4. На освоение нужных для решения поставленной задачи функций и собственно «программирование» было потрачено два дня, затем процесс обработки одного испытания занимал 10-15 минут вместе с печатью протокола.

5. Удобной возможностью пакета MathCad является простое и наглядное документирование всей процедуры обработки, когда данные, программы, расчеты и графики помещены в одном месте. Эту же процедуру/программу элементарно подготовить к публикации в интернете, просто сохранив ее как WEB-страницу.

Литература:

1. Оценка степени деградации ротора серводвигателя с помощью Фурье анализа сигнала тока.
2. Справочник по математике. Г. Корн, Т. Корн. Изд-во «Наука», М., 1973.
3. Основы физики. том 2. Б.М. Яворский, А.А. Пинский, Изд-во «Наука», М., 1974.
4. Методика определения технического состояния и остаточного ресурса асинхронных электродвигателей на напряжение 0,4 кВ. РД ЭО 0343-01.
5. ГОСТ Р 52002-2003. Электротехника. Термины и определения основных понятий.
6. Кацман М.М. Электрические машины: Учеб. для учащихся электротехн. спец. техникумов. - 2-е изд., перераб. и доп. - М.: Высшая школа, 1990.
7. Дьяконов В.П. Компьютерная математика. Теория и практика. М.: Нолидж, 2001.
8. Цифровая обработка сигналов. А.Б. Сергиенко-СПб.: Питер, 2002.